https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
복습 :
🐾 20220922
🐾 20220924
🐾 20220926
🐾 20221014

📌 어디까지 혼자 생각했나?
앞서 풀어본 bfs 문제와 비슷할거라고 생각하고 이차원 리스트와 거리를 저장할 일차원 리스트를 생각했다.
그런데 구현부분에서 어떻게 해야 최솟값을 구할지 모르겠어서 정답을 찾아보았다.
💡 새롭게 알게된것
다익스트라 문제에는 heapq가 사용된다.
heapq는 최소힙을 사용할 수 있는 모듈로
이 힙에 들어가면 가장 작은 원소가 인덱스 0이 된다.
import heapq
heap = []
heapq.heappush(heap,(3,1))
heapq.heappush(heap,(0,2))
heapq.heappush(heap,(2,0))
print(heap)
heapq.heappop(heap)
print(heap)
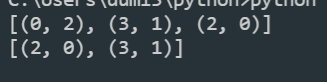
heappop()을 하면 가장 작은 앞의 원소가 반환된다.
💻[코드]
import sys
import heapq
input = sys.stdin.readline
INF = sys.maxsize
V,E = map(int,input().split())
K = int(input())
graph = [[] for _ in range(V+1)] # 정점간 거리 관계를 담을 리스트
dis = [INF]*(V+1) # 최소거리를 담을 리스트
for _ in range(E) :
u,v,w = map(int,input().split())
graph[u].append([w,v]) # heapq에 입력받아서 가중치가 최소인 요소를 찾아야하므로 w먼저
heap = []
def Dijkstra(start):
dis[start] = 0 # 시작점의 최소거리는 0
heapq.heappush(heap,(0,start))
while heap :
wei, node = heapq.heappop(heap)
if dis[node] < wei : continue # 최단거리도 아닌거 볼필요가 없지
for w, new_node in graph[node] :
new_w = w+wei
if dis[new_node] > new_w : # 지금의 새로운 가중치가 작으면 dis에 넣는다.
dis[new_node] = new_w
heapq.heappush(heap,(new_w,new_node))
Dijkstra(K)
for i in range(1,V+1) :
print("INF" if dis[i]==INF else dis[i])
🎨 그래서 큰그림으로 보면?
1. 입력받을 거 다 입력받는다.
2. 가중치와 정점을 입력받을때 큐를 이용해 최솟값을 가장 먼저 찾기위해 [w,v]로 한다.
3. 시작점의 가중치를 0으로 두고 시작
4. graph배열에서 해당 노드와 관련된 노드를 돌면서
5. dis보다 작은 가중치가 있다면 dis를 갱신하고 heap에 넣는다.
6. heap이 빌 때 까지 반복
다익스트라를 c++로 재밌게 풀었던 기억이 있었는데 파이썬으로 봐서 그런가
조금 복잡하네
복습 코드 :
def dijkstra(start) :
q = []
# dist, 현재 위치
heapq.heappush(q,[0,start])
distance[start] = 0
while q :
dist,cur = heapq.heappop(q)
if distance[cur] < dist : continue
# 인접한 노드들 방문
for i in mp[cur] :
# 가중치 더하기
cost = dist + i[1]
# 현재보다 작은 cost라면?
if distance[i[0]] > cost :
distance[i[0]] = cost
heapq.heappush(q,[cost,i[0]])
if __name__=="__main__" :
V,e = map(int,input().split())
k = int(input())
mp = [[] for _ in range(V+1) ]
distance = [int(1e9)]*(V+1)
# 가중치 입력
for _ in range(e) :
u,v,w = map(int,input().split())
mp[u].append([v,w])
dijkstra(k)
# 출력
for i in range(1,V+1) :
print(distance[i] if distance[i]<int(1e9) else "INF" )
<참고 사이트>
https://www.youtube.com/watch?v=F-tkqjUiik0
https://my-coding-notes.tistory.com/200
[🥇5 / 백준 1753 / 파이썬] 최단경로
1753번: 최단경로 첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1≤K
my-coding-notes.tistory.com
https://sungmin-joo.tistory.com/33
[백준] 1753번 최단경로 파이썬 해설 (다익스트라 알고리즘)
출처 : https://www.acmicpc.net/problem/1753 1753번: 최단경로 첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1≤V≤20,000, 1≤E≤300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한..
sungmin-joo.tistory.com
https://www.daleseo.com/python-heapq/
[파이썬] heapq 모듈 사용법
Engineering Blog by Dale Seo
www.daleseo.com
"이 포스팅은 쿠팡 파트너스 활동의 일환으로, 이에 따른 일정액의 수수료를 제공받습니다."
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| [삼성SW역량][Python/BOJ] 백준 14500 테트로미노(DFS) (0) | 2022.06.29 |
|---|---|
| [삼성SW역량][Python/BOJ] 백준 13458 시험 감독(수학)풀이와 수정과정 (0) | 2022.02.10 |
| [Python/BOJ] 백준 14442 벽 부수고 이동하기2(BFS)-시간초과에서 삽질하다가 AC (3) | 2022.01.14 |
| [Python/BOJ] 백준 2206 벽 부수고 이동하기(BFS) (0) | 2022.01.13 |
| [Python/BOJ] 백준 7576 토마토(BFS) (0) | 2022.01.11 |